Análisis y Diseño de Algoritmos
Prof:
Ing. Victor Garro
Asistente: Marco Elizondo
Vargas
Árboles
Arbol
AVL
Los
árboles binarios de búsqueda tal y como los hemos visto, adolecen del problema
de
que
en el peor de los casos pueden tender parcialmente hacia el árbol degenerado,
de manera que la búsqueda de un elemento cualquiera puede ser de un orden
superior a O(lg n), y tender a O(n). Este problema
queda solucionado con los árboles AVL, o balanceados en altura.
Denominados
así en honor a sus autores (Adelson-Velskii y Landis, en una
publicación soviética del año 1.962), estos árboles aseguran una serie de
propiedades que permiten que la búsqueda de cualquier elemento quede acotada
por una complejidad de orden O(lg n), con un
coeficiente de aproximadamente 1'45. El orden de las operaciones de inserción y
eliminación sigue siendo O(lgn). Por tanto, las
aplicaciones de estos árboles son las mismas que las de un ABB, y además puede
emplearse en sistemas en tiempo real en los que es necesario establecer una
cota superior aceptable del tiempo que tardarán en ejecutarse ciertas
operaciones.
Denominamos
árbol AVL a aquél árbol binario de búsqueda que o es vacío, o ambos hijos son también AVL y la diferencia entre
sus alturas es menor o igual que 1.
|
Altura(Hijo_izq(a)) - Altura(Hijo_dch(a))
| # 1
Al
valor | Altura(Hijo_izq(a)) - Altura(Hijo_dch(a)) | lo podemos llamar factor de balance.
La
propiedad que debe cumplir un ArbolBB para ser AVL es
la siguiente:
Es_AVL : ArbolBB
Lógico
ecuaciones r : elemento i, d : ArbolBB
Es_AVL(Crear) == V
Es_AVL(Arbol_binario(r,
i, d)) == Es_AVL(i) and
Es_AVL(d) and
(-1
# Altura(d) - Altura(i) # 1)
and
(not Es_Vacio(i) 6 (r
> Máximo(i))) and
(not Es_Vacio(d) 6 (r
< Mínimo(d)))
El
secreto de conseguir un factor de balance que se mantenga entre los límites
establecidos, se encuentra tanto en el proceso de inserción como de
eliminación. De
fundamental importancia serán las rotaciones a derecha y a izquierda (que no tienen absolutamente nada que ver con sus homónimas en los anillos).
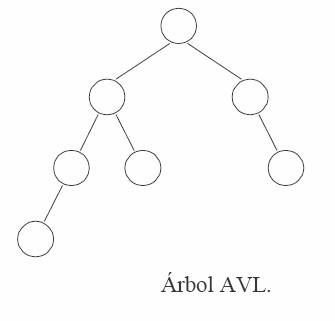
Definición de árbol AVL
Sea T un árbol binario de búsqueda (ABB) con Ti y Td siendo sus subárboles izquierdo y derecho respectivamente, tenemos que:
- Si T es vacío, es un árbol AVL
- Si T es un ABB no vacío, es AVL si (si y sólo si):
- Ti y Td son AVL y
- H(Ti)
− H(Td) = − 1, 0
ó + 1 (factor de equilibrio)
Por esta definición tenemos que el árbol de la figura de arriba no es AVL, mientras que el de abajo sí lo es. Véase también que se trata de un árbol ordenado, en el cual para cada nodo todos los nodos de su subárbol izquierdo tienen un valor de clave menor y todos los nodos de su subárbol derecho tienen un valor de clave mayor que el suyo, cumpliendo así la propiedad de los ABB.
Factor de equilibrio
Cada nodo, además de la información que se pretende almacenar, debe tener los dos punteros a los árboles derecho e izquierdo, igual que los árboles binarios de búsqueda (ABB), y además el dato que controla el factor de equilibrio.
El factor de equilibrio es la diferencia entre las alturas del árbol derecho y el izquierdo:
FE = altura subárbol derecho - altura subárbol izquierdo;
Por definición, para un árbol AVL, este valor debe ser -1, 0 ó 1.
Operaciones
Las operaciones básicas de un árbol AVL implican generalmente el realizar los mismos algoritmos que serían realizados en un árbol binario de búsqueda desequilibrado, pero precedido o seguido por una o más de las llamadas "rotaciones AVL".
Inserción
La inserción en un árbol de AVL puede ser realizada insertando el valor dado en el árbol como si fuera un árbol de búsqueda binario desequilibrado y después retrocediendo hacia la raíz, rotando sobre cualquier nodo que pueda haberse desequilibrado durante la inserción.
Dado que como mucho un nodo es rotado 1,5 veces log n en la vuelta hacia la raíz, y cada rotación AVL tarda el mismo tiempo, el proceso de inserción tarda un tiempo total de O(log n) .
Extracción
El problema de la extracción puede resolverse en O(log n) pasos. Una extracción trae consigo una disminución de la altura de la rama donde se extrajo y tendrá como efecto un cambio en el factor de equilibrio del nodo padre de la rama en cuestión, pudiendo necesitarse una rotación.
Esta disminución de la altura y la corrección de los factores de equilibrio con sus posibles rotaciones asociadas pueden propagarse hasta la raíz.
Búsqueda
 Las
búsquedas se realizan de la misma manera que en los ABB, pero al estar el árbol
equilibrado la complejidad de la búsqueda nunca excederá de O(log n).
Las
búsquedas se realizan de la misma manera que en los ABB, pero al estar el árbol
equilibrado la complejidad de la búsqueda nunca excederá de O(log n).
Antes
de pasar a especificar
estas
operaciones, supondremos que
el
tipo ArbolAVL posee las mismas
operaciones
básicas que el ArbolBB,
o
sea, Crear, Arbol_binario, Raiz,
Hijo_izq e Hijo_dch,
aunque, al igual
que
en el ArbolBB, la operación
Arbol_binario estará oculta al
usuario,
que sólo podrá aumentar el
tamaño
de un árbol mediante la
o p e r a c ió n Inser t a r , cu ya
especificación
veremos más adelante.
Una
vez establecido el marco de
 trabajo,
vamos a ver el significado gráfico de las operaciones Rotar_Izq
y Rotar_Dch, de cuya existencia el usuario no tendrá
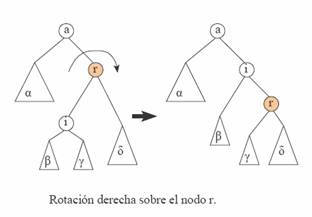
conocimiento: serán auxiliares. Una de tales rotaciones se produce siempre
sobre un nodo determinado; la figura ilustra el resultado de efectuar una
rotación a la derecha sobre el nodo que se halla sombreado. Una rotación a la
derecha sobre un nodo r, con
hijos i y d, consiste en sustituir r por Raiz(i), como hijo izquierdo colocamos a Hijo_izq(i),
y como hijo
trabajo,
vamos a ver el significado gráfico de las operaciones Rotar_Izq
y Rotar_Dch, de cuya existencia el usuario no tendrá
conocimiento: serán auxiliares. Una de tales rotaciones se produce siempre
sobre un nodo determinado; la figura ilustra el resultado de efectuar una
rotación a la derecha sobre el nodo que se halla sombreado. Una rotación a la
derecha sobre un nodo r, con
hijos i y d, consiste en sustituir r por Raiz(i), como hijo izquierdo colocamos a Hijo_izq(i),
y como hijo
derecho
construímos un nuevo árbol que tendrá a r como raíz, y a Hijo_dch(i) y a d como
hijos izquierdo y derecho respectivamente.
Un
hecho muy importante de estas rotaciones, es que mantiene la ordenación del
árbol,
o
sea, si el árbol original era ArbolBB, el resultado
también lo seguirá siendo.
La
especificación de estas operaciones es muy sencilla. Por supuesto, no se
permite rotar al árbol vacío, ni tampoco rotaciones que requieran poner como
raíz final a la raíz de un árbol vacío; en otras palabras:
Rotar_Izq : ArbolAVL
ArbolAVL
Rotar_Dch : ArbolAVL
ArbolAVL
precondiciones a : ArbolAVL
Rotar_Izq(a) : (not
Es_Vacío(a)) and (not Es_Vacío(Hijo_Dch(a))
Rotar_Dch(a) : (not
Es_Vacío(a)) and (not Es_Vacío(Hijo_Izq(a))
ecuaciones r, r' : Elemento i, d, i', d'
: ArbolAVL
Rotar_Izq(Arbol_binario(r,
i, Arbol_binario(r', i', d'))) ==
Arbol_binario(r', Arbol_binario(r,
i, i'), d')
Rotar_Dch(Arbol_binario(r,
Arbol_binario(r', i', d'), d)) ==
Arbol_binario(r', i', Arbol_binario(r,
d', d))
Supongamos
ahora que se hace una inserción o una eliminación según el método
tradicional
del ArbolBB. Nuestra tarea posterior será analizar si
se ha producido un desbalanceo,
y
si es así, entonces poner remedio al asunto para volver a alcanzarlo, de manera
que el árbol
resultante
siga siendo binario de búsqueda, o sea, mediante rotaciones.
Tras
efectuar una de estas operaciones pueden ocurrir diversos casos:
1)
No se ha producido desbalanceo, es
 decir,
a partir de todo nodo, la diferencia de alturas entre sus hijos es menor o
igual que
decir,
a partir de todo nodo, la diferencia de alturas entre sus hijos es menor o
igual que
1.
En este caso no haremos nada. El árbol
sigue
siendo AVL.
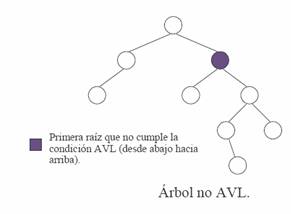
2)
Existe algún nodo que se ha
desbalanceado. Una regla importante es
actuar
sobre el primer nodo que incumpla el factor de balance 1, empezando desde abajo
hacia arriba, o sea, desde las hojas hacia la raíz. P.ej.,
en la figura de antes, actuaremos sobre el nodo sombreado, en lugar de sobre la
raíz directamente.
Sin
pérdida de generalidad, vamos a centrarnos en el caso en que sea el subárbol
izquierdo el de mayor altura h+2,
mientras que el derecho poseerá altura h.
El caso contrario se resuelve de forma especular.
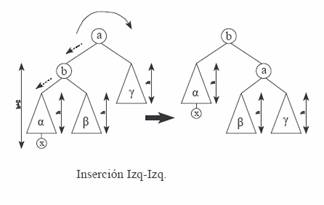
2.1)
Como puede verse en la figura, el árbol de raíz b se halla compensado (hijos de
alturas h+1 y h respectivamente), mientras que el a no. Observamos pues, que el
nodo que produce la descompensación, x,
se insertó por la rama izquierda de a. A su vez, x se ha insertado también a la
izquierda de b. Estamos ante un caso Izquierda-Izquierda (II). Este caso se
resuelve fácilmente efectuando una rotación a derecha sobre el nodo
descompensado a, dando como resultado un árbol AVL.
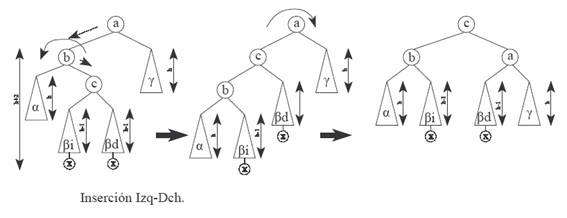
2.2)
Sin embargo, el método anterior no resulta suficiente cuando la inserción es
Izquierda-Derecha, como puede comprobar por sí mismo el lector. En este caso,
habremos de considerar también a la raíz del hijo derecho de b, o sea, a c. Nos dará igual si el nodo x se ha insertado a la derecha o a la izquierda de
c. En el dibujo se ha representado esto colocando x a ambos lados;
el
lector no debe confundirse, la inserción se ha hecho en cualquiera de los dos pero no en ambos; por tanto el factor de
balanceo entre Hijo_izq(c) e Hijo_Dch(c)
es exactamente 1. La solución consiste en dos pasos:
a)
Efectuar una rotación a la izquierda sobre el nodo b.
b)
Efectuar una rotación a la derecha sobre el nodo a.
Los
casos Derecha-Derecha y Derecha-Izquierda se tratan de manera especular o
simétrica.
Manualmente,
para hacer la inserción, iremos marcando con flechitas el camino seguido
por
el nodo a insertar. Una vez incluído el nodo,
seguiremos el camino inverso al recorrido (de abajo arriba), y en el momento en
que nos encontremos un nodo desbalanceado le
aplicaremos las rotaciones correspondientes según el caso. Así sucesivamente
hasta llegar a la raíz.
El
caso de la eliminación debe considerarse como inserción según el camino
opuesto. Es
lo
mismo descompensar una balanza poniendo más peso en un lado que quitando peso
del otro.
De
esta forma, las operaciones Insertar y Eliminar, quedarían:
Insertar
: Elemento × ArbolAVL ArbolAVL
Eliminar
: Elemento × ArbolAVL ArbolAVL
ecuaciones e, r : Elemento i, d, i', d' : ArbolAVL
Insertar(e,
Crear) == Arbol_binario(e, Crear, Crear)
Insertar(e, Arbol_binario(r, i, d)) ==
SI e = r ENTONCES
Arbol_binario(e, i, d)
SI
NO SI e > r ENTONCES
SEA
d' = Insertar(e, d) EN
SI
Altura(d') - Altura(i) <= 1 ENTONCES
Arbol_binario(r, i, d')
SI
NO SI e > Raiz(d) ENTONCES
Rotar_Izq(Arbol_binario(r,
i, d'))
SI
NO
Rotar_Izq(Arbol_binario(r,
i, Rotar_Dch(d')))
SI
NO
SEA
i' = Insertar(e, i) EN
SI
Altura(i') - Altura(d) <= 1 ENTONCES
Arbol_binario(r, i', d)
SI NO SI e < Raiz(i) ENTONCES
Rotar_Dch(Arbol_binario(r, i', d))
SI NO
Rotar_Dch(Arbol_binario(r,
Rotar_Izq(i'), d))
Eliminar(e,
Crear) == Crear
Eliminar(e,
Arbol_binario(r, i, d)) ==
SI
e = r ENTONCES
SI
Es_Vacio(i) ENTONCES
d
SI
NO SI Es_Vacio(d) ENTONCES
i
SI
NO
SEA
d' = Eliminar(Mínimo(d), d) EN
SI
Altura(i) - Altura(d') <= 1 ENTONCES
Arbol_binario(Mínimo(d), i, d')
SI
NO SI Altura(Hijo_izq(i))$Altura(Hijo_Dch(i)) ENT__
Rotar_Dch(Arbol_binario(Mínimo(d),
i, d'))
SI
NO
Rotar_Dch(
Arbol_binario(Mínimo(d),Rotar_Izq(i), d')
)
SI
NO SI e < r ENTONCES
SEA
i' = Eliminar(e, i) EN
SI
Altura(d) - Altura(i') <= 1 ENTONCES
Arbol_binario(r, i', d)
SI
NO SI Altura(Hijo_dch(d)) >= Altura(Hijo_izq(d)) ENTONCES
Rotar_Izq(Arbol_binario(r,
i', d))
SI
NO
Rotar_Izq(Arbol_binario(r,
i', Rotar_Dch(d)))
SI
NO
SEA
d' = Eliminar(e, d) END
SI
Altura(i) - Altura(d) <= 1 ENTONCES
Arbol_binario(r, i, d')
SI
NO SI Altura(Hijo_izq(i)) >= Altura(Hijo_dch(i)) ENTONCES
Rotar_Dch(Arbol_binario(r, i, d'))
SI
NO
Rotar_Dch(Arbol_binario(r,
Rotar_Izq(i), d'))
Al
igual que con los árboles binarios de búsqueda, las operaciones Insertar y
Eliminar
conservan
la propiedad de ser AVL; en otras palabras, se cumple:
teoremas e : Elemento a : ArbolAVL
Es_AVL(a) 6 Es_AVL(Insertar(e, a))
Es_AVL(a) 6 Es_AVL(Eliminar(e, a))
Se
demuestra que, por norma general, cuando el árbol tiene un tamaño decente,
suele ser necesaria una sola rotación por cada 2 inserciones, y una sola rotación
por cada 5 eliminaciones.
Como
puede observarse, todas las operaciones están basadas en la altura de cada
árbol.
Si
cada vez que hacemos una inserción tenemos que calcular y recalcular las
alturas de los árboles, estaremos ante operaciones de complejidad bastante
superior al orden O(lg n). Esto en la especificación
no es ningún problema, ya que en ellas nuestro objetivo es tan sólo expresar el
comportamiento de las operaciones. Sin embargo en las implementaciones supone
un recargo de tiempo considerable. Para solucionar esto, podemos guardar junto
con cada nodo, la altura a que se encuentra, aunque para árboles muy grandes,
esto puede ser un exceso innecesario de memoria.
Otra
solución más factible es utilizar un campo que nos diga únicamente si sus dos
hijos tienen alturas iguales, o quien de los dos tiene mayor altura.
