Análisis y Diseño de Algoritmos                                                                                                      

Prof: Ing. Victor Garro

Asistente: Marco Elizondo Vargas

 

Grafos

 

técnicas básicas de búsqueda

 

BÚSQUEDA EN GRAFOS

Para efectuar una búsqueda de los vértices de un grafo, se pueden emplear dos estrategias diferentes:

Búsqueda en profundidad (BEP): Se comienza en cualquier vértice y en cada paso se avanza a un nuevo vértice adyacente siempre que se pueda. Cuando todos los adyacentes a X hayan sido visitados, se retrocede al vértice desde el que se alcanzó X y se prosigue. Así se consigue etiquetar (visitar) todos los vértices de la componente conexa en que se encuentre el vértice inicial.

Esta técnica se utiliza cuando necesitamos encontrar respuesta a un problema sobre un grafo sin condiciones de optimización.

La idea en general de la búsqueda en profundidad comenzando en un nodo A es la siguiente:

Primero examinamos el nodo inicial A. Luego examinamos cada nodo N de un camino P que comience en A; a sea, procesamos un vecino de A, luego un vecino de un vecino de A y así sucesivamente, hasta llegar a un punto muerto o final del camino P, y de aquí volvemos atrás por P hasta que podamos continuar por otro camino P´ y así sucesivamente.

Este algoritmo es similar al del recorrido inorden de un árbol binario, y también a la forma en que se debe pasar a través de un laberinto. Observe que se hace uso una pila en lugar de una cola, y este es el detalle fundamental que hace la diferencia para realizar la búsqueda en profundidad.

Algoritmo para la búsqueda en profundidad:

Este algoritmo realiza la búsqueda en profundidad el grafo G comenzando en un nodo A.

1. Inicializar todos los nodos al estado de preparado (ESTADO=1)
2. Meter el nodo inicial A en la pila y cambiar su estado a estado de espera (ESTADO=2).
3. Repetir los pasos 4 y 5 hasta que la pila este vacia.
4. Sacar el nodo N en la cima de la pila. Procesar el nodo N y cambiar su

estado al de procesado (ESTADO=3).

5. Meter en la pila todos los vecinos de N que estén en estado de

preparados (ESTADO=1) y cambiar su estado a estado de espera

(ESTADO=2).

[ fin de bucle del paso 3 ]

6. Salir.

nota: tomado del libro Estructura de datos, serie schaum Mcgraw-Hill,

pagina: 337, capitulo: 8 Grafos y sus aplicaciones, autor: Seymour Lipschutz

Búsqueda en anchura (BEA): A diferencia con la BEP ahora se visitan todos los vecinos de un vértice antes de pasar al siguiente. Por tanto no hay necesidad de retroceder. Una vez etiquetados todos los vecinos de un vértice X, se continúa con el primer vértice alcanzado después de X en la búsqueda.

Esta técnica se utiliza para resolver problemas en los que se pide hallar una solución óptima entre varias.

En general la búsqueda en anchura comenzando de un nodo de partida A es la siguiente:

Primero examinamos el nodo de partida A.

Luego examinamos todos los vecinos de A. Luego examinamos todos los vecinos de los vecinos de A y así sucesivamente. Con el uso de una cola, garantizamos que ningún nodo sea procesado más de una vez y usando un campo ESTADO que nos indica el estado actual de los nodos.

Algoritmo para la búsqueda en anchura:

Este algoritmo realiza la búsqueda en anchura en un grafo G comenzando en un nodo de partida A.

1. Inicializar todos los nodos al estado de preparados (ESTADO=1).
2. Poner el nodo de partida A en la COLA y cambiar su estado a espera (ESTADO=2).
3. Repetir pasos 4 y 5 hasta que COLA esté vacía.
4. Quitar el nodo del principio de la cola, N. Procesar N y cambiar su

estado a procesado (ESTADO=3).

5. Añadir a COLA todos los vecinos de N que estén en estado de

preparados (ESTADO=1) y cambiar su estado al de espera

(ESTADO=2).

[ fin del bucle del paso 3 ]

6. Salir.

nota: tomado del libro Estructura de datos, serie schaum Mcgraw-Hill,

pagina: 334 - 335, capitulo: 8 Grafos y sus aplicaciones, autor: Seymour Lipschutz

 

 

 

 

 

Arboles de recubrimiento mínimo (búsqueda del camino más corto):

 CAMINOS MINIMOS EN GRAFOS 

Para lograr el propósito del recorrido mínimo dentro de un grafo G, es necesario para nuestro caso en particular (puesto que no es la única técnica existente) la utilización del algoritmo de WARSHALL para el camino mínimo, el cual se expresa de la forma siguiente:

Sea G un grafo con m nodos, u 1 , u 2 , ..., u m suponga que queremos encontrar la matriz de caminos P para el grafo G. WARSHALL dio un algoritmo para este propósito que es mucho más eficiente que calcular las potencias de la matriz de adyacencia A y aplicar la proposición:

donde sea A la matriz de adyacencia y P = Pij la matriz de caminos de un grafo G entonces, Pij = 1 si y solo sí hay un numero positivo en la entrada ij de la matriz

Este algoritmo de WARSHALL se usa para calcular el camino mínimo y existe un algoritmo similar para calcular el camino mínimo de G cuando G tiene peso.

Algoritmo de WARSHALL:

Un grafo dirigido G con M nodos está en memoria por su matriz adyacente A, este algoritmo encuentra la matriz de caminos (Booleana) P del grafo G.

1. [ Inicializar P ] repetir para I, J =1, 2, ... M:

si A[ I, J ]=0, entonces: hacer P[ I, J ]:=0;

si no: hacer P[ I, J ]:=1.

[ fin de bucle ]

2. [ Actualizar P ] repetir paso 3 y 4 para K=1, 2, ..., M:
3. repetir paso 4 para I=1, 2, ..., M:
4. repetir para J=1, 2, ..., M:

hacer P[ I, J ]:= P[ I, J ] V ( P[ I, J] ^ P[ K, J ]).

[ fin de bucle ]

[ fin de bucle paso 3 ]

[ fin de bucle paso 2 ]

5. Salir.

nota: tomado del libro Estructura de datos, serie schaum Mcgraw-Hill,

pagina: 322, capitulo: 8 Grafos y sus aplicaciones, autor: Seymour Lipschutz

Algoritmo de matriz de camino mínimo:

Cuando se trata de un grafo con peso G de M nodos está memoria mediante su matriz de peso W; este algoritmo encuentra la matriz Q tal que [ I, J ] es la longitud del camino mínimo del nodo VI al nodo VJ . INFINITO es un número muy grande y MIN es la función del valor mínimo.

1. [ Inicializar Q ] repetir para I, J=1, 2, . . ., M:

si W [ I, J ] = 0, entonces: hacer Q [ I, J ]:= INFINITO;

si no: hacer Q [ I, J ] := W [ I, J ].

[ fin de bucle ]

2. [ Actualizar Q ] repetir pasos 3 y 4 para K=1, 2, . . ., M:
3. repetir paso 4 para I = 1, 2, . . ., M:
4. repetir para J = 1, 2, . . ., M:

hacer Q [ i, J ] := MIN(Q [ i, J ]+ Q [ i, K ]+ Q [ K, J ]).

[ fin de bucle ]

[ fin de bucle del paso 3 ]

[ fin de bucle del paso 2 ]

5. Salir.

nota: tomado del libro Estructura de datos, serie schaum Mcgraw-Hill,

pagina: 324, capitulo: 8 Grafos y sus aplicaciones, autor: Seymour Lipschutz

Enunciado para ejemplo: 

Dado un grafo simple no dirigido, conexo y ponderado de n nodos etiquetados con los números naturales desde el 1 hasta el n, se numeran los ejes desde 1 hasta m de acuerdo con el orden. Dados a continuación dos nodos cualesquiera, se trata de encontrar el camino más corto entre ambos nodos, utilizando el algoritmo de Dijkstra.

Entrada: En la primera línea, un número natural que indica el número de casos que se van a plantear. Para cada caso, una línea con el número de nodos n del grafo, y la representación decimal del mismo (entero menor que ) separados por un blanco. En la siguiente línea, separados por blancos, m números naturales que representan los pesos de los ejes del grafo. En la siguiente línea, otro número natural p nos dice cuantos pares de nodos se van a proponer, y a continuación aparecen en líneas diferentes y separados por blancos todas estas parejas.

Salida: Para cada uno de los casos propuestos, el fichero de salida contendrá una línea indicando el caso de que se trata en la forma Grafo # con el símbolo # sustituido por el número del caso. Las siguientes m líneas contendrán la lista de adyacencias del grafo en la forma:

siempre separando con blancos y con los nodos adyacentes en orden creciente de número. A continuación, p líneas que resuelven las p parejas de nodos planteadas, componiendo cada línea en la forma:

Ejemplo de Entrada: 

2

4 49

53 82 53

2

1 2

1 3

8 14728196

81 48 30 64 71 13 91 10 65

3

2 1

4 1

8 1

Ejemplo de Salida: 

Grafo 1

1 2 53

2 1 53 4 82

3 4 53

4 2 82 3 53

53 1 2

188 1 2 4 3

Grafo 2

1 4 81

2 6 48 7 30 8 64

3 4 71 6 13

4 1 81 3 71 8 91

5 6 10 7 65

6 2 48 3 13 5 10

7 2 30 5 65

8 2 64 4 91

213 2 6 3 4 1

81 4 1

172 8 4 1

Algoritmo de Dijkstra: Este algoritmo construye el árbol de caminos de longitud mínima entre un vértice fijado V y los restantes vértices en un grafo ponderado.

Observaciones:

1. Los pesos de las aristas deben ser no negativos.
2. El algoritmo de Dijkstra NO proporciona un árbol generador mínimo.

 

Ordenación Topológica:

Hasta recientemente todos los trabajos sobre Topología (Digital principalmente) se basaban en un enfoque de Teoría de Grafos. Este enfoque presenta, sin embargo, el problema de determinar la relación de adyacencia más razonable en Zn. Actualmente existen enfoques alternativos basados en nociones de Topología General. En este caso haremos una introducción a algunos de estos enfoques.

Topología definición:

1) Rama de la matemática que estudia las propiedades del espacio que son invariantes por homeomorfismos. Se trata de propiedades no métricas, es decir, de propiedades cualitativas, y no cuantitativas, lo que la distingue de la geometría común. Se la suele denominar "geometría débil" o "geometría del caucho". Por ejemplo, una circunferencia es topológicamente equivalente a un cuadrado, por más que sus propiedades métricas sean diferentes

2) Una topología en un conjunto X es una familia de subconjuntos de X que satisface ciertos axiomas (ver espacio topológico).

En esta sección estudiaremos las diferentes estrategias que se han planteado principalmente motivadas por problemas en el área del reconocimiento de formas para dotar a la digitalización D de un conjunto, de una estructura, no necesariamente explícitamente topológica, en términos de la cual formular propiedades de D relacionadas con las propiedades de la imagen original.

Las imágenes 2-dimensionales son las mas ampliamente estudiadas, aunque últimamente las 3-dimensionales están siendo muy utilizadas. También se utilizan imágenes 4-dimensionales para representar imágenes 3-dimensionales en movimiento.

De las estrategias planteadas, la primera y las más utilizada es la introducida por Azriel Rosenfeld en 1970. Se basa en la noción de adyacencia entre puntos de Zn (además de Zn también considera en ocasiones los centros de una teselación del plano por hexágonos). Su enfoque descansa principalmente en nociones de Teoría de Grafos.

Desde entonces la Topología Digital ha proporcionado los fundamentos teóricos para importantes operaciones de procesamiento de imagen, como recuento de objetos, adelgazamiento de imágenes, detección de bordes y relleno de contornos. El adelgazamiento de imágenes es una operación de preprocesamiento en reconocimiento de formas. Su objetivo es reducir el conjunto de puntos de la imagen sin alterar la topología de la misma.

Ordenación topológica:

Suponga que S es un grafo tal que cada nodo vi de S representa una tarea y cada arista ( u, v ) significa que la finalización de la tarea u es un pre-requisito para que comience la tarea v. Suponga que tal grafo S contiene un ciclo tal que:

P=( u, v, w, u )

Esto significa que no podemos empezar v hasta completar u, no podemos empezar w hasta terminar v y no podemos empezar u hasta completar w. Así no podemos completar ninguna tarea del ciclo. Por tanto, un grafo S así, que representa tareas y relaciones de precedencia, no puede tener ciclos.

Ahora suponga que S es un grafo sin ciclos, considere la relación < sobre S definida como sigue:

u < v si existe un camino de u a v

Esta relación tiene las siguientes tres propiedades:

1. Para cada elemento u de S, tenemos que u < u. ( Irreflexivilidad )
2. Si u < v, entonces v < u. ( Asimetría )
3. Si u < v y v < w, entonces u < w. ( Transitividad )

Tal relación < sobre S se llama ordenación parcial de S, y S con tal ordenación se llama conjunto parcialmente ordenado o conjunto po. Así, un grafo S sin ciclos se puede considerar un conjunto parcialmente ordenado.

Por lo tanto, puede también suponer que si S es un conjunto parcialmente ordenado con la ordenación parcial denotada por <, entonces S se puede considerar un grafo cuyos nodos son los elementos de S y cuyas aristas están definidas como sigue:

( u, v ) es una arista en S si u < v

más aun, se puede demostrar que un conjunto S parcialmente ordenado, considerado como un grafo, no tiene ciclos.

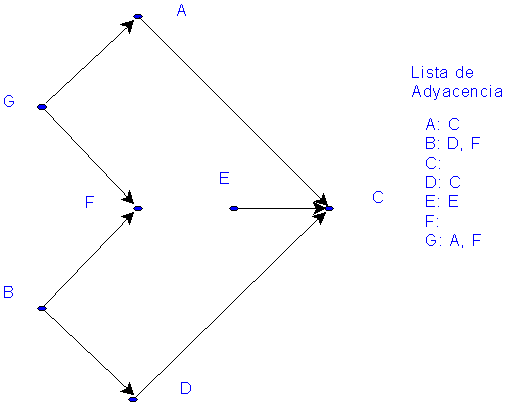Como ejemplo podemos plantear que: sea S el grafo de la figura, observe que S no tiene ciclos. Así S se puede considerar un conjunto parcialmente ordenado. Note que G < C, ya que existe un camino desde G hasta C. Similarmente, B < F y B < C. Por otro lado B no es menor que A, ya que no existe camino de B a A, al igual que A no es menor que B.

Por lo tanto; sea S un grafo dirigido sin ciclos (o conjunto parcialmente ordenado). Una ordenación topológica T de S es una ordenación lineal de los nodos de S que preserva la ordenación parcial de S original, o sea, que si u < v en S (si hay un camino de u a v en S), entonces u va delante de la v el la ordenación lineal T, este se muestra en la siguiente figura, donde se incluyen las aristas para indicar que concuerdan con la dirección de la ordenación lineal.

Información adicional sobre Topología:

Topología combinatoria:

Rama de la topología que reduce el estudio de curvas y superficies a ciertos esquemas determinados por polígonos curvilíneos, evitando de esta forma pensarlas como conjuntos de puntos, como lo hace la topología conjuntista. El tratamiento combinatorio es más cercano al álgebra, y reduce el concepto de homeomorfismo a unas pocas reglas que permiten decidir cuándo dos esquemas combinatorios son equivalentes.

Topología inducida:

Dado un subconjunto A de un espacio topológico X, se llama topología inducida a la topología definida en A que toma como abiertos a todos los conjuntos de la forma U Ç A, en donde U es un abierto de X. En estas condiciones, se dice que A es un subespacio de X.

Topología usual:

La topología usual del espacio n–dimensional (Rn) tiene como abiertos básicos a las bolas n–dimensionales (abiertas). Es decir, un conjunto de Rn es abierto si y sólo si es unión de cierto número de bolas abiertas. Equivalentemente, diremos que A es abierto si y sólo si para todo punto x Î A existe una bola B contenida en A tal que x Î B (A es entorno de x).

Toro:

Se llama así a la superficie de revolución engendrada por la rotación de una circunferencia en torno a un eje que no la toque en ninguno de sus puntos. Si bien esta definición es geométrica, las propiedades topológicas del toro son de gran importancia. En especial, la propiedad de tener un asa, o agujero, que determina que existan en el toro lazos no reducibles. Un importante teorema de la topología combinatoria asegura que toda superficie cerrada y orientable es un toro con n agujeros. El caso n = 0 corresponde obviamente a la esfera, si se la piensa como un "toro sin agujeros", y el caso n = 1 es el toro usual. Si bien la definición habitual del toro lo presenta como una superficie sumergida en el espacio tridimensional, es fácil ver que es homeomorfo al producto cartesiano de dos circunferencias, sumergido en R4 (espacio cuatridimensional). Es decir, la definición topológica del toro es: T2 = S1 ´ S1. Esto permite generalizar, y definir al toro n–dimensional como el producto cartesiano de n circunferencias, es decir: Tn = S1 ´ ... ´ S1.

En la topología combinatoria, el toro bidimensional se define identificando dos a dos los lados opuestos de un rectángulo, como muestra la figura:

 

 

 

Algoritmo de ordenación topológica:

El siguiente algoritmo encuentra una ordenación topológica T de un grafo S sin ciclos.

1. Encontrar el grado de entrada GraEnt(N) de cada nodo N de S (se puede hacer recorriendo cada lista de adyacencia)
2. Poner en una cola todos los nodos con grado de entrada nulo.
3. Repetir los pasos 4 y 5 hasta que la cola esté vacía.
4. Quitar el nodo N al frente de la cola (haciendo Frente:=Frente + 1)
5. Repetir lo siguiente para cada vecino M de N:

Hacer GraRnt(M):= GraEnt(M) – 1 (esto elimina la arista de N a M)

si GraEnt(M)=0, entonces: Añadir M al final de la cola.

[ fin de bucle paso 5 ]

[ fin de bucle paso 3 ]

6. Salir.

nota: tomado del libro Estructura de datos, serie schaum Mcgraw-Hill,

pagina: 340, capitulo: 8 Grafos y sus aplicaciones, autor: Seymour Lipschutz